foobar2000:Components/VST 2.4 adapter (foo_vst)
Deprecated component
This component was deprecated in favor of a new VST adapter (foo_dsp_vst3) developed by Peter Pawlowski. While you can use this component, it is recommended (especially new users) to use Peter's new VST adapter instead.
| VST 2.4 adapter | |
|---|---|
 VST 2.4 adapter | |
| Developer(s) | Yegor Petrov |
| Repository | GitHub |
| Release information | |
| Initial release | November 13, 2010; 14 years ago |
| Stable release | 0.9.0.3 (March 5, 2011) |
| foobar2000 compatibility | |
| Architecture | x86 32-bit |
| Minimum version | 1.0 |
| UI module(s) | N/A |
| Additional information | |
| Use | DSP |
| View all legacy components | |
VST 2.4 adapter is a component which aims to allow Foobar2000 users to use VST 2.4 plug-ins equally with “native” ones. Thousands of freeware and commercial DSP plug-ins are available in this format.
Contents
Usage
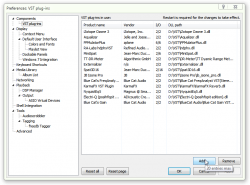
First, add VST plug-ins you would like to use in the VST manager: Preferences → Components → VST plug-ins. Restart is required for the changes to take effect. After the restart open the DSP Manager or some conversion dialog box to try the plug-ins you've added.
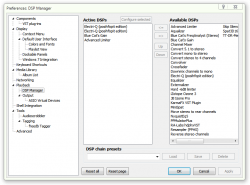
Use View → DSP menu to access DSP configuration windows. Bind commands by their number to keyboard shortcuts if necessary.
VST program file (.fxp) import/export items are in the system menu of editor windows (right click on the window's titlebar).
Microsoft Visual C++ 2008 Redistributable Package (x86) may be required for versions below 0.8.1
Download
See the attachment in the first post of the discussion thread.
Features
The component has support for the following feature set:
- Multiple instances
- Multiple channels (including asymmetric configs like 2.0 → 5.1)
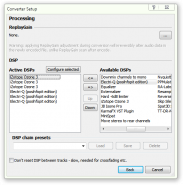
- Chain presets and secondary DSP chains (“convert” feature)
- Modeless DSP configuration windows with keyboard shortcut binding
- FXP import/export
Limitations and known issues
- Limited to 20 VST entries due to API limitations (not to be confused with particular instances in a chain).
- No support for VSTs without custom editors yet (to be implemented in the near future).
- Display goes ahead of audio by the size of the output buffer.
- No x64 VST support: Foobar2000 is a 32-bit application. However, most effect plug-ins are available as 32 bit binaries.
- Modeless DSP configuration functionality isn't well synchronized with the DSP manager in the Preferences window.
- There are two versions labeled as v1.0 and v1.0.01 which are actually v0.1 and v0.2.
- At least older 0.9.0.3 version can cause playing mono files in only one channel
Most of these problems are caused by diametrically opposite approaches to the management of DSP objects lifetime. In contrast to VST, Foobar2000 assumes plug-in's user interface to be highly decoupled from the DSP code and the most difficult task solved by the adapter is coupling things back. Actually, such kind of DSPs as analyzers in fb2k is even impossible due to lack of connection between the GUI and audio rountines (of course one can have analyzers in form of visualization, but it's out of processing chain then). Foobar2000 recreates DSP objects whenever settings or playback state is changed, while in VST plug-ins are supposed to be loaded only once and their settings are to be changed directly with either automation or a editor window. Also in VST, plug-ins rely on their host in respect of number of channels, but in Foobar2000 it's the other way round, i.e. the host renders as many channels as a plug-in has. Finally, VST host must provide a window for the plug-in to create a editor and it's not supposed to block windows underneath while Foobar2000 requires config windows to be modal, etc.
Given all this, it must be clear that something had to be sacrificed for the sake of features listed above in the article. The adapter keeps track of current DSP chain to ensure proper threading and gapless playback, it abuses programming language features to overcome “one DSP service per class” principle, it adds random data to presets and looks for a window title before opening a editor to distinguish different instances of the same VST effect, it has advanced settings to deal with some other problems as well. In many ways the adapter's reliability is limited by these tricks, yet there are many faulty VST plug-ins around.
Important notes
- The adapter doesn't scan plug-ins at startup nor does it track changes in the VST directory. If some plug-in is absent then the adapter bypasses its processing.
- The component stores its settings in a separate binary file because of API limitations.
Settings
This component has only advanced settings placed in the corresponding section of Foobar2000 preferences. Depending on the component version they can be found either in the Playback or VST category (the latter is true for v0.6+). All the problems that mentioned here are caused by the differences between Foobar2000 and VST approaches to DSP implementation.
- Declicker size (256*n samples, 4 by default)
- Number of zero samples to be passed through VST on transport switches to suppress plug-in's output data that can produce click at the beginning of the next track, i.e. ringing of filters or delay effect tail. The latter requires this number to be increased. Changes to this setting take effect after restart.
- Limit number of outputs
- In contrast to DAW, audio players don't manage outputs of their DSPs. Besides, many VST plug-ins don't report activity of their outputs. Hence the only way to output data from 16-channel VST is to drop some of the channels according to the setting.
- VST idle time to unload DLL (0-10,000 ms) (0.7.1 and below)
- The delay is needed to suppress excessive unload-load cycles between tracks, i.e. to keep VST plug-ins loaded as it is supposed to be for them. In 0.8 the [un]loading strategy was revamped and this setting isn't necessary anymore.
Change log
0.9.0.3
- Fixed removal on the player updates
0.9
- Support for conversion and playback with same DSP chain presets
- Preset manager for each VST
- Per-instance channel number limit
- DSP config shortcuts bugfixes
0.8.1.0
- Revamped VST [un]loading strategy with regard to threading issues.
- Doesn't use registry anymore (hold Shift and press Add button to get VST entries back).
0.7.1
- Bugfixes in the portable mode support.
0.7.0
- Serious bugfixes.
- Relative paths in portable mode.
0.6.0
- Added FXP export/import.
- Improved View → DSP menu.
- Introduced declicker.
0.52
- Fixed the bug which could lead to crash after stopping the playback
0.51
- Added experimental support for no-reload track switching.
0.5
- Added experimental support for non-modal config dialogs (View → DSP).
- Added some formal procedures for some capricious plug-ins to work.
- Added output number limitation setting
0.2
- Fixed major stability issues. Marked as v1.00.01.
0.1
- Initial release marked as v1.0. Very unstable.
External links
- Discussion topic on
 hydrogenaudio
hydrogenaudio
- KVR: Audio Plug-in Database
- VST in Wikipedia