Difference between revisions of "Fast Fourier Transform"
From Hydrogenaudio Knowledgebase
m (Removed anonymous edits made March/April 2022 from a particular range of IP addresses) |
|||
| (17 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Fast Fourier | + | '''Fast Fourier transform''' ('''FFT''') is an efficient algorithm for calculating the [[DFT|discrete Fourier transform]] (DFT). The FFT produces the same results as a DFT but it reduces the execution time by hundreds in some cases. Whereas DFT takes an order of <math>O(n^2)\,</math> computations, FFT takes an order of <math>O(n\,\log\,n)</math>, and is definitely the preferred algorithm to be used in all applications in terms of computational complexity. The FFT in most implementations consistent of samples that are exactly a power of 2, this is commonly known as a ''FFT Radix 2'' algorithm where <math> n = 64,128,256,512,1024,2048</math> etc. |
| + | |||
| + | ==External links== | ||
| + | * {{wikipedia|Fast Fourier transform}} | ||
| + | |||
| + | [[Category:Signal Processing]] | ||
| + | [[Category:Technical]] | ||
Latest revision as of 12:45, 18 August 2023
Fast Fourier transform (FFT) is an efficient algorithm for calculating the discrete Fourier transform (DFT). The FFT produces the same results as a DFT but it reduces the execution time by hundreds in some cases. Whereas DFT takes an order of 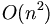 computations, FFT takes an order of
computations, FFT takes an order of 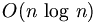 , and is definitely the preferred algorithm to be used in all applications in terms of computational complexity. The FFT in most implementations consistent of samples that are exactly a power of 2, this is commonly known as a FFT Radix 2 algorithm where
, and is definitely the preferred algorithm to be used in all applications in terms of computational complexity. The FFT in most implementations consistent of samples that are exactly a power of 2, this is commonly known as a FFT Radix 2 algorithm where 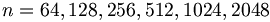 etc.
etc.
External links
- Fast Fourier transform on Wikipedia