Difference between revisions of "Fast Fourier Transform"
From Hydrogenaudio Knowledgebase
Beardgoggles (Talk | contribs) m (Added external links section.) |
|||
| (14 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Fast Fourier | + | '''Fast Fourier transform''' ('''FFT''') is an efficient algorithm for calculating the [[DFT|discrete fourier transform]] (DFT). The FFT produces the same results as a DFT but it reduces the execution time by hundreds in some cases. Whereas DFT takes an order of <math>O(n^2)\,</math> computations, FFT takes an order of <math>O(n\,\log\,n)</math>, and is definitely the preferred algorithm to be used in all applications in terms of computational complexity. The FFT in most implementations consistent of samples that are exactly a power of 2, this is commonly known as a ''FFT Radix 2'' algorithm where <math> n = 64,128,256,512,1024,2048</math> etc. |
| + | ==External links== | ||
| + | * {{wikipedia|Fast Fourier transform}} | ||
| + | [[Category:Signal Processing]] | ||
[[Category:Technical]] | [[Category:Technical]] | ||
Revision as of 20:48, 24 July 2019
Fast Fourier transform (FFT) is an efficient algorithm for calculating the discrete fourier transform (DFT). The FFT produces the same results as a DFT but it reduces the execution time by hundreds in some cases. Whereas DFT takes an order of 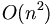 computations, FFT takes an order of
computations, FFT takes an order of 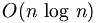 , and is definitely the preferred algorithm to be used in all applications in terms of computational complexity. The FFT in most implementations consistent of samples that are exactly a power of 2, this is commonly known as a FFT Radix 2 algorithm where
, and is definitely the preferred algorithm to be used in all applications in terms of computational complexity. The FFT in most implementations consistent of samples that are exactly a power of 2, this is commonly known as a FFT Radix 2 algorithm where 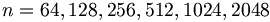 etc.
etc.
External links
- Fast Fourier transform on Wikipedia