Difference between revisions of "Fast Fourier Transform"
From Hydrogenaudio Knowledgebase
(<math>-ify the expressions) |
m (... that's not true. Most FFT algorithms are power 2 based, however there can be mixed radix implementations ;-D) |
||
| Line 1: | Line 1: | ||
| − | Fast Fourier Transform is an efficient algorithm for calculating the discrete fourier transform ([[DFT]]). Reduces the execution time by hundreds in some cases. Whereas [[DFT]] takes an order of <math>O(n^2)\,</math> computations, FFT takes an order of <math>O(n\,\log\,n)</math>, and is definitely the preferred algorithm to used in all applications. The | + | Fast Fourier Transform is an efficient algorithm for calculating the discrete fourier transform ([[DFT]]). Reduces the execution time by hundreds in some cases. Whereas [[DFT]] takes an order of <math>O(n^2)\,</math> computations, FFT takes an order of <math>O(n\,\log\,n)</math>, and is definitely the preferred algorithm to used in all applications. The FFT in most implementations consistent of samples that are exactly a power of 2. |
| − | [[Category: | + | [[Category:Algorithms]] |
Revision as of 21:22, 2 September 2006
Fast Fourier Transform is an efficient algorithm for calculating the discrete fourier transform (DFT). Reduces the execution time by hundreds in some cases. Whereas DFT takes an order of 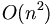 computations, FFT takes an order of
computations, FFT takes an order of 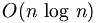 , and is definitely the preferred algorithm to used in all applications. The FFT in most implementations consistent of samples that are exactly a power of 2.
, and is definitely the preferred algorithm to used in all applications. The FFT in most implementations consistent of samples that are exactly a power of 2.